前一天講完了演算法的分類，今天將會深入講解各個學派以及相對應的演算法。

貝式推理統計學派

貝式推理學派以統計學中的條件概率為推理核心，此學派認為「因果關係是一個概率問題」，一件事情發生的概念不是如一般統計學發生的頻率多寡來決定，而是要決定於相關的其他變數發生的概率高低，才能藝起來診斷該事件發生的可能性之高低。

貝式推理基本概念

利用已知相關事件的證據，亦即先驗概率來推導出我們對某一事件或假說的相信程度。例如:信用卡的刷卡特徵，在一天內頻繁刷卡、快速多筆小額刷卡等等特徵，並推論出此筆交易可能為盜刷事件。

貝式定理(Bayes'Theorem)

P(A|B)=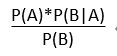

若以台灣50歲婦女為例為例:
P(COVID|Positive):若快篩檢查為陽性，那麼得到covid的概率有多高?這是我們預測最關心的問題。
P(COVID):此為已經知道的事實，稱為先線概率(Prior Probability)。例如:女性得COVID的概率。
P(Positive | COVID)：指真的為COVID的話，則快篩為陽性的概率為多少，即快篩的準確率，舉例95％。
P(Positive)：指被檢驗成偽陽性的機率。

貝氏定理主要觀點

• 概論是依據推導的
• 概率是假設的驗證
• 重視尋找原因（果->因）

樸素貝式定理

要判斷整個事件的特徵有許多，比如說要判斷是不是covid有許多特徵，例如：發燒、喉嚨痛、肌肉酸痛、咳嗽、味覺異常等等，這些症狀並不是獨立發生，而是互相影響的，若要估算各種組合的機率，會造成組合太多，加上不同的病人有不同的症狀，將會無法搜集全部的樣本，造成無法估算。為了解決這個問題，樸素貝式定理把每個變數之間視為獨立，亦即covid發生的概率將由每個症狀的貝式定理相乘總和算出來，沒有症狀之間的互動與組合的問題，公式如下：

P(Covid｜喉嚨痛、發燒、肌肉痠痛、咳嗽、味覺異常）
＝P(喉嚨痛｜Covid) P(發燒｜Covid) P(肌肉酸痛｜Covid) P(咳嗽｜Covid) P(味覺異常｜Covid)

當每個症狀出現機率高時，則罹患Covid的機率也高。

貝式推理應用

• 洗錢交易判斷
• 信用卡盜刷判斷
• 文章分類

貝式推理優點

• 簡單而強大
• 正確程度高
• 用途廣
• 彈性大
• 樣本不苛求
• 易理解複雜問題
• 解釋力強

貝式推理缺點

• 不適用特徵有強烈關聯之問題
• 要先計算所有概率
• 難處理結構性問題

參考資料
人工智慧-概念應用與管理 林東清著